インターネットの様々なところで使われている公開鍵暗号方式の大多数は、RSA暗号化方式を利用している。この方式は1977年に発明され、発明者であるRonald Linn Rivest、Adi Shamir、Leonard Max Adlemanの頭文字をとってRSAとしている。
RSA暗号化方式で使用されている暗号問題は何種類かあるが、現在最も使われているのは素因数分解問題(FP:factoring problem)である。
FPはフェルマーの小定理に基づいて設計されており、p を素数とし、a を p の倍数でない整数(a と p は互いに素)とするときに、a^(p−1)≡1 (mod p) すなわちaのp−1乗をpで割った余りは 1 であるというもの。
FPは、素数と素数をかけ合わせて生成した数値を素因数分解することが現代のコンピュータにとって難しいことを利用している。
つまりFPベースのRSA暗号の強度のカギとなるのは素因数分解の難易度であり、nからn=p・qとなる素数p, qを求める問題を解くためにかかる時間が十分に長いものであれば安全だということになる。
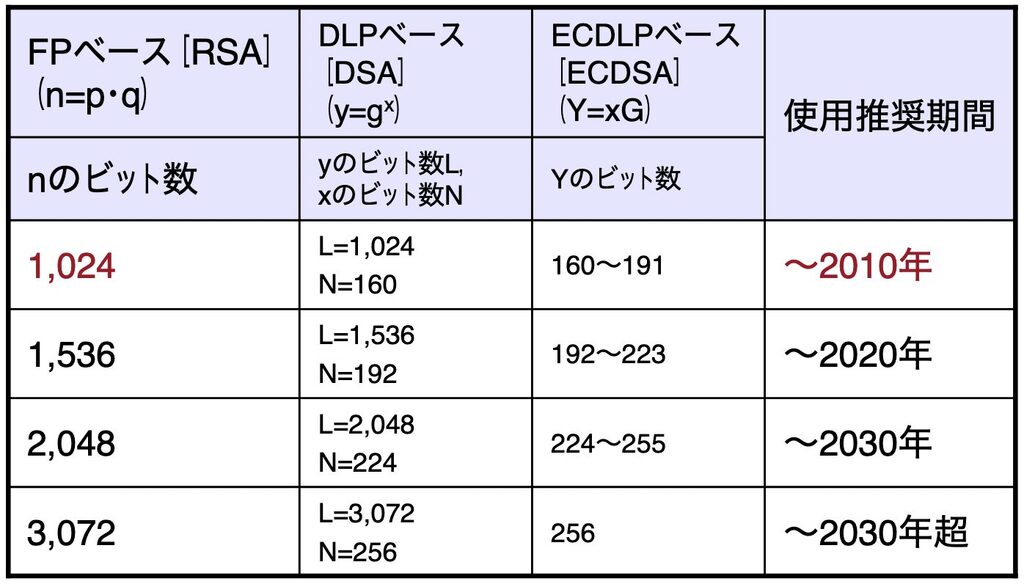
コンピュータの処理能力は年々向上しており、現在は2,048ビット以上の利用が推奨されている。それ未満だと安易に解読されてしまう可能性が高まっているためだ。
SSHで利用する秘密鍵・公開鍵のペアを生成する一般的なコマンド ssh-keygen は現在デフォルトで(特にオプション指定が無い場合)、2,048ビットのRSA暗号を生成するが、個人的には -b オプションを用いて4,096ビット以上の鍵長を使用している。
量子コンピュータを使えば簡単に素因数分解問題は解けてしまうが、鍵長に応じて量子コンピュータの必要ビット数も多くなる。例えば1,024(2^10)ビットのRSA暗号を解くためには2*10=20qubit(量子ビット)が必要となるが、スーパーコンピュータでは1万年かかる計算が、グーグルの53量子ビットのマシンなら200秒で済むということになる。
IBMは2023年リリースを目標に、1,000qubitの量子コンピュータを製作中だ。こうなるともうRSA暗号は桁数を増やしても安全とはいえない時代を迎える。FPベースのほか、DLPベース(離散対数問題)、ECDLPベース(楕円離散対数問題)などの離散対数問題(あるいはDiffie-Hellman問題)も同様に、量子計算に対しては無力だ。
量子コンピュータによる解読を防ぐためには、量子コンピュータによって解読が困難な暗号化方式にするしかない。これを対量子暗号という。現在は格子暗号が最も有力な候補だ。
しかし現実的な問題は、どんなに強力な暗号化方式が登場しようとも、脆弱な暗号化が利用可能なままのシステムが無数に存在していることだ。
コンピュータ技術の発展に合わせて、数年前には安全とされていた方式が裸同然になる。一般の方にとっては、何を更新すれば安全で、何を更新したら危険なのかがわかりにくい。
IT技術には、作る側だけが知っていればよいものと、使う側にも知ってもらう必要のある知識があり、この分類はITと生活が密着した現代、とても大切なものだ。



コメント