n次元におけるtorus, wave, time, Fourier transformation,
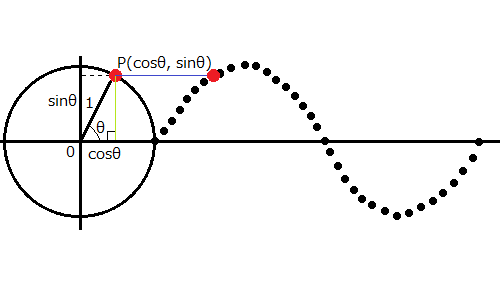
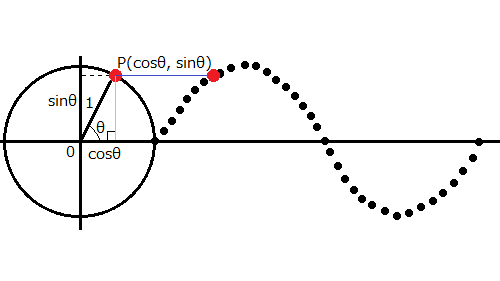
全ての関数は正弦波で表すことができる(三角関数を用いて表現することができる)。
Convergence → torus
Become a sphere in 3 dimensional space. 3次元では球体
4次元では?
波が粒子化するのは円環の収束(集束)
超電導→核力の影響を受けない
波と波の干渉。
例示。二重スリットで双方を抜けた可能性の波が【干渉】し合う座標系(interference space)において、円環の調和する条件の粒子化について考えてみよう。波動が0の状態では粒子化は起きない。波動関数によって示されるすべての存在可能性の波。これは最適化すればmoduloであり、ある数によって円環の法則が確認できる。これはたとえばmod 5であれば0から4までの世界の繰り返しである。mod 5の波動を三次元で表してみるとその回転による重ね合わせは5で適合することになる。(素数・素数においては基本的に重ね合わせはひとつであるということが証明できれば、素数のもつ性質を新しい視点で観察することができる)
それでは円環の調和はどのポイントで起きるのか? (pos)(pos), (neg)(neg)は(pos)である。(pos)(neg)は(neg)つまり3dwにおいては打ち消し合うような物理的観測結果を生むのでこれは観察によって粒子化が観測できないエネルギー状態になったという説明に収束する。しかしこれは粒子化していない状態ではないので特殊角として考慮しておく価値をもつ。
二次元的波動の収束による波の物質化の次元数観点からみた評価について。2次元の波が収束してみるとそれは大局的(macro)にみれば次元の消失(2→1)で点に収束しているが局所的(micro)にみれば次元の昇華(2→3)である。これはどちらも正しく、単なるperspectiveによる観察の変化と捉えることができるし、これが物性の真理に近づくヒントといえよう。2次元世界における1次元的な波(線)の収束ポイントは0次元(点)であるが、実際にそこに現れる物質は点であると同時に2次元的質量(面積)をもつことを観測できる。この事実を観測すると、あたかも1次元的な線が0次元的に交差した座標から2次元的な面が発生したように見える。その考え方で3次元世界における観測を適用すれば、3次元世界における2次元的な波の収束は線をなすが、実際にそこに現れる物質は球あるいはそれに準じた三次元的特性を観察可能な対象である。その波動のさらに上の次元の性質を、重ね合わせの波の性質が表すと仮定できる。
その条件に調和はあるのか?あるとすれば、観察意識による認識との関連性を無視することができないが、現時点で次元の認識が限定されている状況下の説明になるのでそこは無視する。二次元の波動が収束する際に起きる昇華の説、その次元超越のエネルギー分布の可能性を示すひとつの鍵が、数学的にみて円環の調和をとるかどうか。そこにはプランク定数が関わる。つまり、1/∞の現宇宙における物理法則に合致する物質化が発生するキーはプランク定数で示される。そこで、当然ながら定数の異なる環境下における観測可能な物質化の世界を想定することができる。


コメント